Práctica 6. Regresión múltiple 2

Materiales de la sesión del 19 Jun 2020

Índice

Objetivo de la práctica
Resumen Práctica 6:
Reporte de progreso
Foro práctica 6

Objetivo de la práctica

En esta práctica nos enfocaremos en el significado de las parcializaciones en la regresión múltiple. Para ello utilizaremos el ejemplo 3.1 de Wooldrige (2010) cap. 3 (Análisis de regresion múltiple) (p.68-80) sobre las determinantes del promedio en la universidad.

Librerías

pacman::p_load(ggpubr, #graficos
               dplyr, #manipulacion de datos
               sjPlot, #tablas
               gridExtra, #unir graficos
               texreg, #mostrar regresion multiple
               summarytools, #estadisticos descriptivos
               wooldridge) #paquete con los ejemplos del libro
library(wooldridge)

Datos

Los datos a utilizar corresponden a la base de datos gpa1 que incluye una muestra de 141 estudiantes de una universidad. La base contiene variables:

$colGPA$: promedio general de calificaciones de la universidad, en escala de 0 a 4 puntos.
$hsGPA$ : promedio general de calificaciones en la enseñanza media, en escala de 0 a 4 puntos
$ACT$ : puntaje en el examen de admisión a la universidad, que va de 16 a 33 puntos

Primero, se cargará la base de datos que contiene la librería wooldrige y se seleccionarán las variables señaladas

data('gpa1') # Cargar base de datos
gpa1 <- dplyr::select(gpa1, colGPA, hsGPA, ACT) #Seleccion de variables

Explorar base de datos

A partir de la siguiente tabla se obtienen estadísticos descriptivos que luego serán relevantes para la interpretación de nuestros modelos.

view(dfSummary(gpa1, headings = FALSE, method = "render"))

## Warning in png(png_loc <- tempfile(fileext = ".png"), width = 150 *
## graph.magnif, : X cannot set locale modifiers

## Warning in png(png_loc <- tempfile(fileext = ".png"), width = 150 *
## graph.magnif, : X cannot set locale modifiers

## Warning in png(png_loc <- tempfile(fileext = ".png"), width = 150 *
## graph.magnif, : X cannot set locale modifiers

No	Variable	Stats / Values	Freqs (% of Valid)	Valid
1	colGPA [numeric]	Mean (sd) : 3.1 (0.4) min < med < max: 2.2 < 3 < 4 IQR (CV) : 0.5 (0.1)	19 distinct values	141 (100%)
2	hsGPA [numeric]	Mean (sd) : 3.4 (0.3) min < med < max: 2.4 < 3.4 < 4 IQR (CV) : 0.4 (0.1)	16 distinct values	141 (100%)
3	ACT [integer]	Mean (sd) : 24.2 (2.8) min < med < max: 16 < 24 < 33 IQR (CV) : 4 (0.1)	15 distinct values	141 (100%)

Generated by summarytools 0.9.6 (R version 4.0.0)
2020-08-20

Relacion entre variables

Se grafican la relación entre las variables que determinarían $colGPA$ para comparar sus distribuciones y sus pendientes ($b$) de sus regresiones simples. A su vez, se grafica un tercer gráfico que muestra la correlación entre las variables independientes.

#Grafico x1 = ACT y= colGPA
gact <- ggscatter(gpa1, x = "ACT", y = "colGPA",
          shape = 21, size = 3, # Forma y tamaño de puntos
   add = "reg.line", #Agregar recta de regresion
   cor.coef = TRUE)# Agregar coeficiente correlacion
#Grafico x2 = hsGPA y= colGPA
ghsGPA <- ggscatter(gpa1, x = "hsGPA", y = "colGPA",
          shape = 21, size = 3,
   add = "reg.line",
   cor.coef = TRUE)

#Grafico x2 = hsGPA x1 = ACT
gact_hs <- ggscatter(gpa1, x = "hsGPA", y = "ACT",
          shape = 21, size = 3,
   add = "reg.line",
   cor.coef = TRUE)

grid.arrange(gact, ghsGPA, gact_hs, nrow = 1) # Unir graficos

Con el gráfico anterior podemos notar dos puntos relevantes:

Si bien ambas variables tienen una asociación positiva con $colGPA$, el tamaño efecto de esta relación es distinta. Incluso, $hsGPA$ que no había sido considerada en nuestro modelo inicial, tiene una asociación más grande con nuestra variable dependiente.
Como es de esperar, existe una relación entre las calificaciones en la enseñanza media ($hsGPA$) y el puntaje en la prueba de admisión ($ACT$). Específicamente, ambas variables tienen una asociación positiva de 0.35.

En la práctica 5 nos preguntamos ¿cómo incide $ACT$ y $hsGPA$ en conjunto sobre $colGPA$?, sin profundizar en qué implica que nuestros predictores de $colGPA$ estén correlacionados. Retomemos nuevamente nuestro modelo

Modelo de regresión multiple

Para estimar el modelo de regresión multiple se debe realizar el mismo procedimiento de la regresión simple, solo que ahora deben señalar un (+) y el segundo predictor

Regresión múltiple modelo <- lm(y ~ x1 + x2 , data = data)

Por fines de comparación, se estimaran primero dos regresiones simples con cada predictor, y luego la regresión múltiple en el Modelo 3:

col_actmodel<-lm(colGPA ~ ACT, data=gpa1)
col_hsmodel<-lm(colGPA ~  hsGPA, data=gpa1)
col_model <- lm(colGPA ~ ACT + hsGPA, data = gpa1)

sjPlot::tab_model(list(col_actmodel, col_hsmodel,col_model), show.ci=FALSE, p.style = "asterisk", dv.labels = c("Modelo 1", "Modelo 2", "Modelo 3"),string.pred = "Predictores", string.est = "β")

	Modelo 1	Modelo 2	Modelo 3
Predictores	β	β	β
(Intercept)	2.40 ^***	1.42 ^***	1.29 ^***
ACT	0.03 ^*		0.01
hsGPA		0.48 ^***	0.45 ^***
Observations	141	141	141
R² / R² adjusted	0.043 / 0.036	0.172 / 0.166	0.176 / 0.164
p<0.05 p<0.01 * p<0.001

\[\widehat{colGPA} = 1.29 +0.01 \dot\ ACT + 0.453\dot\ hsGPA \]

Interpretación

¿Cómo se interpreta este cuadro con los 3 modelos de regresión?

El modelo 1 estima que por cada punto que aumenta el examen de admisión $ACT$, $colGPA$ aumentaráen 0.03 puntos.

El modelo 2 estima que por cada punto que aumenta las notas en enseñanza media $hsGPA$, $colGPA$ aumentará en 0.48 puntos.

El modelo 3 estima $colGPA$ considerando en conjunto ambas variables. Por un lado, por cada punto que aumenta el examen de admisión $ACT$, $colGPA$ aumentaráen 0.01 puntos, manteniendo $hsGPA$ constante Por otro, por cada punto que aumenta las notas en enseñanza media $hsGPA$, $colGPA$ aumentará en 0.45 puntos, manteniendo $ACT$ constante.

¿Porqué se alteran los coeficientes de regresión?

Como vimos en los gráficos de dispersión, existe una correlación entre nuestros predictores: el puntaje en $ACT$ está asociado con las notas de enseñanza media $hsGPA$.

Cuando se incorporan más variables en el modelo se descuenta este elemento en común que tienen las variables independientes. Por ello no solo los coefientes de regresión se ajustan en presencia de otras variables ($hsGPA$ disminuyó de 0.48 a 0.45 y $ACT$ de 0.03 a 0.01), sino que también el ajuste del modelo cambia ($R^2ajustado$ es el estadístico más óptimo para identificar ello, pues como vimos en la práctica 5 $R^2$ sobreestima la bondad de ajuste).

Parcialización

La forma de hacer este procedimiento de “mantener constante” el efecto de la otra variable se llama parcialización. Este procedimiento implica sacar la covarianza común entre mis variables independientes, es decir, lo que tienen en compun $hsGPA$ y $ACT$

Se habla de efectos parciales porque se estiman las regresiones solo con una de las variables independientes. Por ejemplo, ¿Cómo se predice $colGPA$ en función $ACT$, despejando el efecto de $hsGPA$?

En fórmula podemos ver que las estimaciones de $ b_{1}$ y $ b_{2}$ se interpretan como efectos parciales, de manera que dados los cambios en $ACT$ y $hsGPA$ se puede obtener un cambio predicho para $colGPA$.

\[\triangle{colGPA} = b_{1}\triangle{ACT} + b_{2}\triangle{hsGPA} \]

Pero cuando $hsGPA$ se mantiene constante, de manera que $\triangle{hsGPA}$ = 0, se obtiene entonces:

\[\triangle{colGPA} = b_{1}\triangle{ACT} \]

Pero cuando $ACT$ se mantiene constante, de manera que $\triangle{ACT}$ = 0, se obtiene entonces:

\[\triangle{colGPA} = b_{2}\triangle{hsGPA} \]

Parcializar $ACT$ de $hsGPA$

¿Cómo determinar cuál es el (a) elemento común entre ambas variables y (b) extraer solamente aquello que no comparten?

Para ello se realiza (a) una regresión simple donde los predictores son las variables del modelo ($ACT$ dependiente y $hsGPA$ independiente) y (b) en donde a la predicción de $ACT$ hay asociado un residuo.

En otras palabras, el $b$ de esta regresión es todo lo que comparte $ACT$ y $hsGPA$. Mientras que el residuo es todo lo de $ACT$ que no es explicado po $hsGPA$. En síntesis, es con lo que nos deberíamos quedar en nuestros modelos de regresión múltiple al estimar el $b_{1}$ de $ACT$.

Paso 1: Estimar modelo

model_act_hs = lm(ACT ~ hsGPA, data = gpa1) #Crear regresion con predictores
coef(model_act_hs)

## (Intercept)       hsGPA 
##   13.696763    3.074331

En consecuencia tenemos que \[\widehat{ACT} = 13.69 + 3.07{hsGPA} \]

Paso 2: calcular valores predichos y residuos

Sabemos que si tenemos un modelo de regresión podemos también obtener los residuos. Recordemos ¿qué es un residuo? Un residuo es la diferencia entre el valor observado y el valor predicho

fit_act_hs=fitted.values(model_act_hs) # Calcular valores predichos
res_act_hs=residuals(model_act_hs) #Calcular residuos
gpa1=cbind(gpa1, fit_act_hs,res_act_hs) # Unir columna de residuos y valores predichos a base de datos
head(gpa1) #Mostrar los primeros elementos de la base de datos

##   colGPA hsGPA ACT fit_act_hs res_act_hs
## 1    3.0   3.0  21   22.91975 -1.9197550
## 2    3.4   3.2  24   23.53462  0.4653787
## 3    3.0   3.6  26   24.76435  1.2356469
## 4    3.5   3.5  27   24.45692  2.5430797
## 5    3.6   3.9  28   25.68665  2.3133472
## 6    3.0   3.4  25   24.14949  0.8505125

Podemos ver en res_act_hs la varianza no explicada de $hsGPA$ sobre $ACT$.

Paso 3: Crear regresión con variable parcializada

Ahora si hacemos la regresión con la variable res_act_hs notaremos que obtendremos el mismo $b_{1}$ de la regresión del modelo múltiple (modelo 3) pero por medio de una regresión simple (modelo 4).

act_hs_model <- lm(colGPA ~ res_act_hs, data = gpa1) # Estimar regresión simple con parcialización de ACT

sjPlot::tab_model(list(col_actmodel, col_hsmodel,col_model, act_hs_model), show.ci=FALSE, p.style = "asterisk", dv.labels = c("Modelo 1", "Modelo 2", "Modelo 3", "Modelo 4"),string.pred = "Predictores", string.est = "β")

	Modelo 1	Modelo 2	Modelo 3	Modelo 4
Predictores	β	β	β	β
(Intercept)	2.40 ^***	1.42 ^***	1.29 ^***	3.06 ^***
ACT	0.03 ^*		0.01
hsGPA		0.48 ^***	0.45 ^***
res_act_hs				0.01
Observations	141	141	141	141
R² / R² adjusted	0.043 / 0.036	0.172 / 0.166	0.176 / 0.164	0.005 / -0.003
p<0.05 p<0.01 * p<0.001

Lo que tengo en ese modelo es la variable puntaje en el examen de admisión $ACT$ sin las notas de enseñanza media $hsGPA$. Lo mismo se podría realizar con la parcialización de $hsGPA$.

Este procedimiento de extraer el elemento común entre las variables es el que hace “tras bambalinas” la regresión múltiple. Lo importante es notar que en la regresión múltiple todos los predictores están parcializados del resto de los predictores. Se han “limpiado” de los efectos de las otras variables el resto de las variables del modelo.

Control estadístico

¿En cuál variable me fijo para la interpretación? Podemos graficar los coeficientes de la regresión de modo de ver el impacto que tienen cada una de las variables sobre $colGPA$

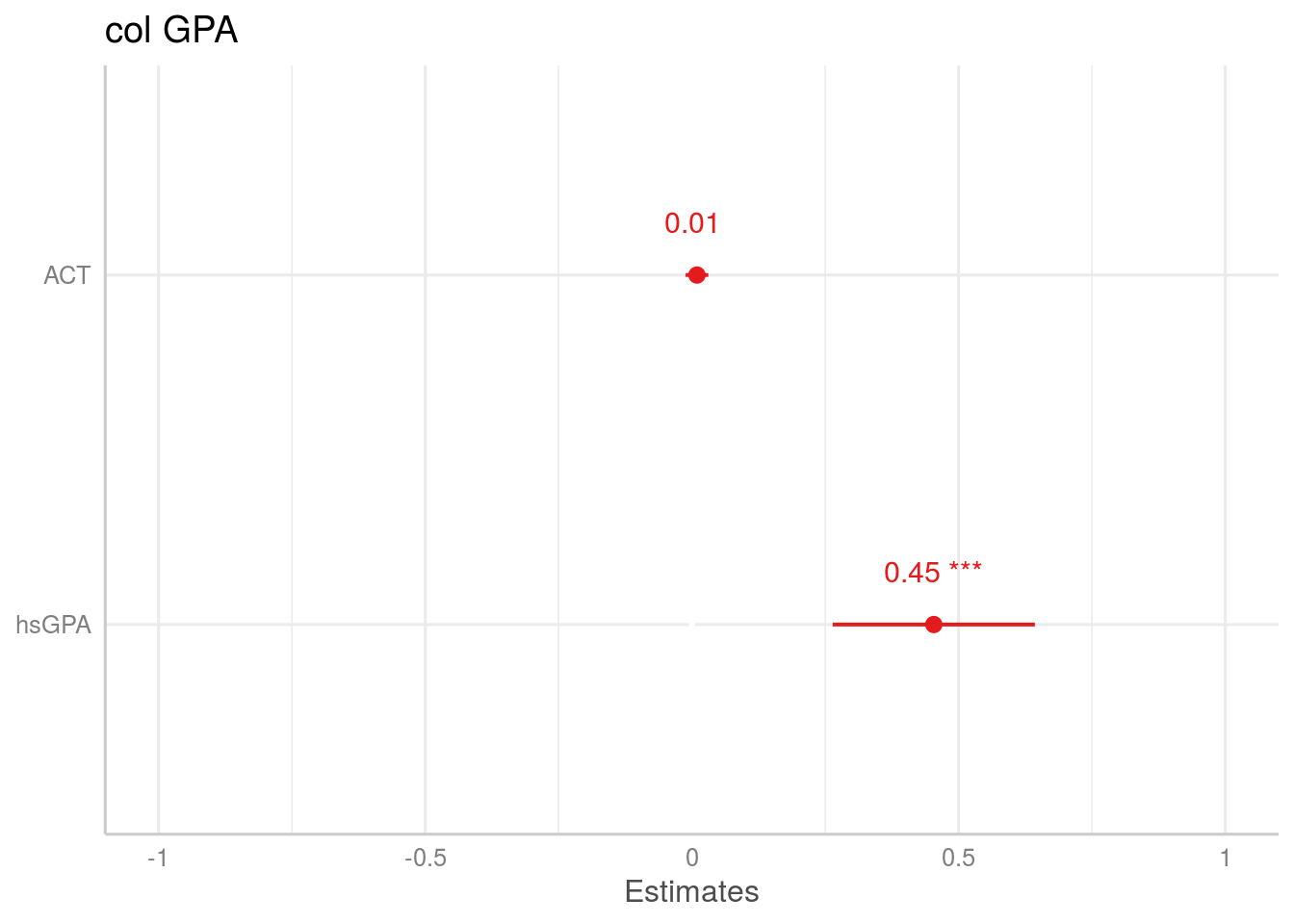
plot_model(col_model, show.values = TRUE)+ theme_sjplot()

Como podemos ver el efecto que tiene $hsGPA$ sobre $colGPA$, controlando por $ACT$, es mucho mayor que el que tiene $ACT$ parcializado por $colGPA$. Sin embargo, esto nada nos dice de qué variable enfatizar: esto dependen de las hipótesis que queremos probar con nuestros modelos.

¿Qué significa mantener todos los demás factores constantes?

En la interpretación del modelo vimos que los coeficientes de regresión nos permiten entender el efecto de $ACT$ sobre $colGPA$, manteniendo $hsGPA$ constante. También, $hsGPA$ sobre $colGPA$, manteniendo $ACT$ constante.

La regresión múltiple nos proporciona esta interpretación “manteniendo constante las variables”, incluso cuando en nuestros mismos datos no hayan sido recoltados de manera constante. Esto es lo que hemos llamado una interpretación de efecto parcial de los coeficientes de regresión. Esto no implica que se haya encuestado personas con el mismo $hsGPA$ pero con puntuaciones en $ACT$. Para obtener los datos no se pusieron restricciones sobre los valores muestrales de $hsGPA$ o de $ACT$. Más bien, la regresión múltiple permite imitar esta situación “constante” sin restringir los valores de ninguna de las variables independientes.

Resumen Práctica 6:

En esta práctica revisamos los siguientes contenidos - Repaso de regresión lineal múltiple - Parcialización - Control estadístico

Reporte de progreso

Completar el reporte de progreso correspondiente a esta práctica [https://forms.gle/mMmR8qZxVJ1uYeUw8]

Foro práctica 6

Last updated on August 21, 2020