Práctica 8. Tabla de regresión múltiple
Índice
En el siguiente documento se presenta un ejemplo de análisis e interpretación de una tabla de regresión múltiple, para que sea considerado como referencia en la entrega de los informes 2 y 3. El ejemplo está adaptado de https://stats.idre.ucla.edu/stata/output/regression-analysis/
Datos
Los datos a utilizar corresponden a resultados de pruebas de conocimiento en distintas areas de 200 estudiantes de educación secundaria.
Ajustes y descriptivos
Primero seleccionamos las variables que vamos a usar en el ejemplo y cambiamos las etiquetas de las variables a español.
## [1] "id" "female" "race" "ses" "schtyp" "prog" "read"
## [8] "write" "math" "science" "socst"data <- data %>% select (science,math,female, socst, read)
data <- data %>% rename(ciencia=science, matematicas =math, mujer=female, status=socst, lectura=read)| No | Variable | Stats / Values | Freqs (% of Valid) | Graph | Valid | Missing | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ciencia [numeric] | Mean (sd) : 51.9 (9.9) min < med < max: 26 < 53 < 74 IQR (CV) : 14 (0.2) | 34 distinct values | 200 (100%) | 0 (0%) | |||||||||||||
| 2 | matematicas [numeric] | Mean (sd) : 52.6 (9.4) min < med < max: 33 < 52 < 75 IQR (CV) : 14 (0.2) | 40 distinct values | 200 (100%) | 0 (0%) | |||||||||||||
| 3 | mujer [numeric] | Min : 0 Mean : 0.5 Max : 1 |
|
200 (100%) | 0 (0%) | |||||||||||||
| 4 | status [numeric] | Mean (sd) : 52.4 (10.7) min < med < max: 26 < 52 < 71 IQR (CV) : 15 (0.2) | 22 distinct values | 200 (100%) | 0 (0%) | |||||||||||||
| 5 | lectura [numeric] | Mean (sd) : 52.2 (10.3) min < med < max: 28 < 50 < 76 IQR (CV) : 16 (0.2) | 30 distinct values | 200 (100%) | 0 (0%) |
Generated by summarytools 0.9.6 (R version 4.0.0)
2020-07-15
Modelos de regresión
Lógica de presentación de modelos
La forma en que se presentan los modelos en regresión múltiple depende de las hipótesis que se estan contrastando, y de la definición del/a investigador/a sobre cuáles son los predictores principales y cuáles son las variables de control. Pensemos en este caso que nuestra hipótesis principal es que el puntaje de ciencias se puede predecir con los puntajes de matemáticas y lectura, pero queremos controlar estas asociaciones por sexo y estatus. En este caso, podríamos presentar dos modelos, uno solamente con los predictores principales, y luego un segundo modelo con los controles para ver si los efectos se mantienen. También podríamos pensar en tres modelos: uno con matemáticas, otro con ciencias, y otro con ambos y además controles. La decisión de cómo presentar los modelos depende principalmente de las hipótesis que se están contrastando, y también de que los resultados permitan hacer la mejor discusión posible.
Estimación
Vamos a estimar un primer modelo con las variables asociadas a la hipótesis principal, y luego un segundo con las variables control:
\[ \text{ciencia} = \alpha + \beta_{1}(\text{matematicas}) + \beta_{2}(\text{lectura}) + \epsilon \]\[ \text{ciencia} = \alpha + \beta_{1}(\text{matematicas}) + \beta_{2}(\text{lectura}) + \beta_{3}(\text{mujer}) + \beta_{4}(\text{status}) + \epsilon \]
Para estimar estos modelos en R:
reg1 <- lm(ciencia ~ matematicas + lectura, data=data)
reg2 <- lm(ciencia ~ matematicas + lectura + mujer + status, data=data)Para presentar los resultados de regresión existen diferentes librerías en R, como stargazer, texreg, sjPlot. En este caso vamos a utilizar la función tab_model de sjPlot:
| ciencia | ciencia | |||||
|---|---|---|---|---|---|---|
| Predictors | Estimates | CI | p | Estimates | CI | p |
| (Intercept) | 11.62 | 5.59 – 17.64 | <0.001 | 12.33 | 6.03 – 18.62 | <0.001 |
| matematicas | 0.40 | 0.26 – 0.54 | <0.001 | 0.39 | 0.24 – 0.54 | <0.001 |
| lectura | 0.37 | 0.23 – 0.50 | <0.001 | 0.34 | 0.19 – 0.48 | <0.001 |
| mujer | -2.01 | -4.03 – 0.01 | 0.051 | |||
| status | 0.05 | -0.07 – 0.17 | 0.424 | |||
| Observations | 200 | 200 | ||||
| R2 / R2 adjusted | 0.478 / 0.473 | 0.489 / 0.479 | ||||
Esta tabla tiene las opciones por defecto. En general, para cada predictor hay dos piezas de información importante: la estimación del coeficiente de regresión \(\beta\) (estimates), y una estimación referida a inferencia/significación estadística (en este caso CI, intervalo de confianza). Esta segunda información es en general el error estándar, pero también puede ser t (que es el coeficiente dividido por el error estándar), o el intervalo de confianza, dado usualmente por el \(\beta\) +/- 1.96 SE para un 95% de confianza (como aparece en esta tabla). Según el output, la información de inferencia puede aparecer abajo del coeficiente, o al lado como en esta tabla.
Abajo vamos a hacer algunos ajustes en la tabla, presentando el error estándar en lugar del intervalo, y reemplazando la columna del nivel de probabilidad de error (p) por asteriscos que indican el nivel de significación de cada coeficiente, lo cual hace más rápida la interpretación. También cambiamos algunas etiquetas de la tabla para que sea más fácil de leer:
sjPlot::tab_model(list(reg1,reg2),
show.se=TRUE,
show.ci=FALSE,
digits=3,
p.style = "asterisk",
dv.labels = c("Modelo 1", "Modelo 2"),
string.pred = "Predictores",
string.est = "β")| Modelo 1 | Modelo 2 | |||
|---|---|---|---|---|
| Predictores | β | std. Error | β | std. Error |
| (Intercept) | 11.616 *** | 3.054 | 12.325 *** | 3.194 |
| matematicas | 0.402 *** | 0.073 | 0.389 *** | 0.074 |
| lectura | 0.365 *** | 0.066 | 0.335 *** | 0.073 |
| mujer | -2.010 | 1.023 | ||
| status | 0.050 | 0.062 | ||
| Observations | 200 | 200 | ||
| R2 / R2 adjusted | 0.478 / 0.473 | 0.489 / 0.479 | ||
|
||||
Y para presentar en forma de ecuaciones, quedaría de la siguiente manera:
\[ \text{ciencia} = 11.62 + 0.4(\text{matematicas}) + 0.37(\text{lectura}) + \epsilon \]\[ \text{ciencia} = 12.33 + 0.39(\text{matematicas}) + 0.34(\text{lectura}) - 2.01(\text{mujer}) + 0.05(\text{status}) + \epsilon \]
Para transformar automáticamente las estimaciones de regresión en R a ecuaciones:
Esto se puede hacer si se utiliza RMarkdown (no es requisito en este curso, para los interesad_s pueden revisar material del curso ciencia social abierta )
Instalar librería equatiomatic. No está en CRAN, así que para instalar:
remotes::install_github("datalorax/equatiomatic")La función para extraer la ecuación es
extract_eq, por ejemplo:extract_eq(reg1)Para que el resultado pueda ser
renderizadodesde un documento RMarkdown a pdf o html, debe estar en un chunk con las siguientes especificaciones:
```{r results='asis', echo=FALSE}
extract_eq(reg1)
extract_eq(reg2)
```- Para presentar las ecuaciones con los coeficientes ya estimados,
extract_eq(reg1, use_coefs = TRUE)
Interpretación
Los coeficientes nos hablan de la relación entre las variables independientes y la variable dependiente. Nos muestran la magnitud del cambio predicho en el puntaje de ciencia por cada 1 unidad en que aumenta el predictor.
Para matematica el coeficiente es de 0.402 en el modelo 1 y baja a 0.389 en el modelo 2. Entonces, por cada punto adicional en la prueba de matemáticas en el modelo 2 se presenta un incremento de 0.389 en el puntaje de ciencia, manteniendo todas las demás variables constantes. Respecto a la inferencia, existen distintas maneras de dar cuenta de la significación estadística. Por ejemplo, se puede decir que este valor es estadísticamente significativo con un 99,9% de confianza, o con una probabilidad de error p<0.001.
Para reportar estos resultados de manera más resumida siguiendo las indicaciones de reporte de APA (American Psychological Association): El puntaje en matemáticas predice significativamente el puntaje de ciencias (modelo 1), b = -.40, SE = .07, p < .001, controlando por el puntaje en lectura. Al agregar los controles de sexo y estatus (modelo 2), el puntaje en matemáticas disminuye levemente pero mantiene su nivel de significación, b = -.39, SE = .07, p < .001.
Con respecto a lectura, en el modelo 2 es posible observar un coeficiente de 0.335. Esto implica que por cada unidad que aumenta el puntaje de lectura se predice un incremento de 0.335 puntos en ciencia, manteniendo todas las demás variables contantes. El coeficiente es estadísticamente significativo con una probabilidad de error p<0.001.
Para la variable mujer podemos observar que el coeficiente tiene un valor de -2.010 en el modelo 2. Al ser mujer una variable dicotómica donde 1 es mujer y 0 es hombre, la estimación nos indica que para las mujeres el puntaje predicho promedio en ciencias es -2.010 puntos más bajo con respecto al promedio de los hombres, manteniendo todas las demás variables constantes. En términos exclusivamente estadísticos, la variable mujer no es significativamente distinta de 0 cuando empleamos un nivel de confianza del 95%, debido a que el valor \(p\) es mayor a 0.05.
Si observamos el coeficiente de status tenemos un valor de 0.050. Entonces, por cada unidad en que incrementa el estatus se predice un incremento de 0.050 puntos en ciencia, manteniendo todas las demás variables constantes. Sin embargo, no es estadísticamente significativo a un 95% de confianza.
Std Error: Esta columna corresponde a los errores estándar de los coeficientes de regresión (Estimate). Estos errores estándar son empleados para testear en qué medida los coeficientes son distintos de 0. El procedimiento es dividir el coeficiente por su error estándar para obstener el valor \(t\), los que luego se contrastan con la tabla de valores críticos t para obtener la probabilidad de error (que ya aparece automáticamente en la tabla) . Además, los errores estándar pueden ser utilizados para calcular los intervalos de confianza.
Una manera de presentar los resultados de un modelo de regresión es a través de la visualización de los coeficientes de regresión con sus respectivos intervalos de confianza. La ventaja de este tipo de gráficos es que podemos observar la magnitud del coeficiente y las “barras de error” que representan el intervalo de confianza inferior y superior. Utilizando un intervalo de confianza de 95% de confianza:
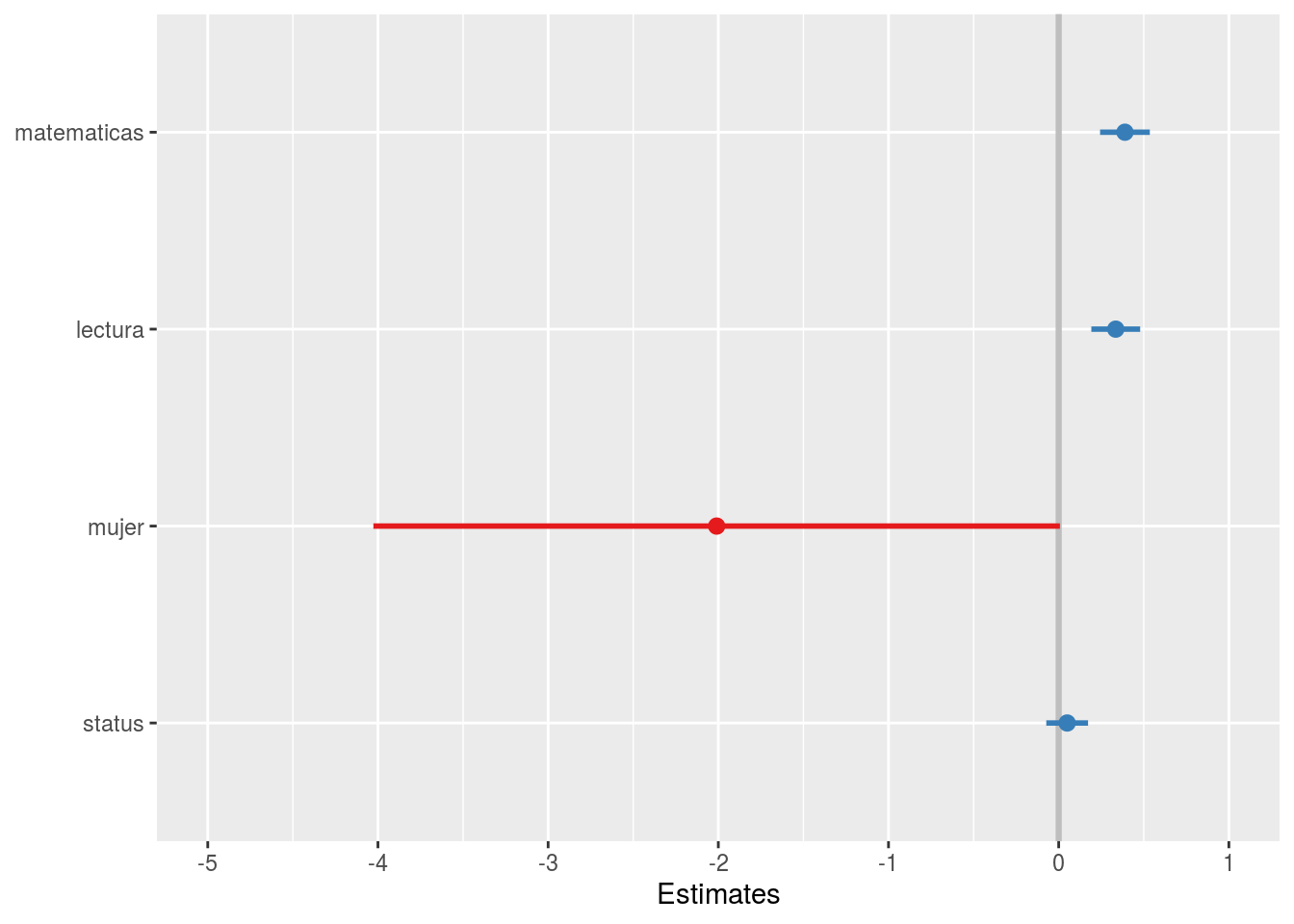
Figure 1: Modelo 2
Lo que nos muestra este gráfico es el valor del coeficiente en el punto, y en las líneas que salen del punto se extienden según su intervalo de confianza. De acuerdo a las reglas de inferencia en regresión, lo que estamos contrastando es que el valor de este coeficiente es distinto de 0 en la población, con un cierto valor de probabilidad. Por lo tanto, si agregamos un intervalo de confianza (valores probables) asociado a una probabilidad de error, entonces podemos decir que este coeficiente es estadísticamente distinto de 0 en la población. Y en el gráfico, esto sucede cuando los intervalos no tocan el 0.
Ajuste global del modelo
R2: El R2 (R-cuadrado) es la proporción de la varianza de la variable dependiente (ciencias) la cual puede ser predicha por las variables independientes (matemáticas, mujer, estatus, lectura). En la Tabla 1 tenemos que para el Modelo (1), este valor nos indica que un 47,7% de la varianza en el puntaje de ciencias se asocia a matemáticas. Luego, en el Modelo (2), el R-cuadrado nos indica que el 48,9% de la varianza de ciencias puede ser predicha conjuntamente por las variables independientes matemáticas, lectura, mujer y status. Como vemos, la incorporación de controles aporta levemente al R2, lo cual se relaciona con que estos predictores no son estadísticamente significativos.
Adjusted R2: En la medida que se incorporan predictores al modelo, cada uno va contribuyendo a explicar la varianza de la variable dependiente. Así, se podría continuar agregando predictores al modelo, incrementando la capacidad explicativa pero también de cierto modo debido a la variabilidad adicional en una muestra particular con la que estemos trabajando. Por esta razón, el R-cuadrado ajustado busca demostrar un valor estimado más realista del R-cuadrado para la población bajo análisis, penalizando por la inclusión de predictores adicionales. En el caso del Modelo (2) de la Tabla 1, el valor del R-cuadrado es de 0.489, mientras que el R-cuadrado ajustado es de 0.479, el cual es calculado a través de la fórmula \(1 – ((1 – R^2)((N – 1) /( N – k – 1))\).
Entonces, si el número de observaciones (\(N\)) es pequeño y el número de predictores (\(k\))es grande, tendremos una mayor discrepancia entre el R-cuadrado y el R-cuadrado ajustado. Por otro lado, cuando el número de observaciones es grande en contraste con el número de predictores tendremos que el valor del R-cuadrado y el R-cuadrado ajustado serán mucho más similares debido.
Por lo tanto, al momento de realizar la intepretación corresponde basarse en los coeficientes del R2 ajustado.
Referencias
Bruin, J. 2006. newtest: command to compute new test. UCLA: Statistical Consulting Group. https://stats.idre.ucla.edu/stata/ado/analysis/.